オイラーツアー
概要
木構造のデータを DFS 順に探索を行い、通った順番で記録する手法。
頂点に注目するものと辺に注目するものがある。
LCA(最近共通祖先: 根付き木において 2 つの頂点の共通祖先で最も深さが大きい頂点) を求めること等に利用できる。
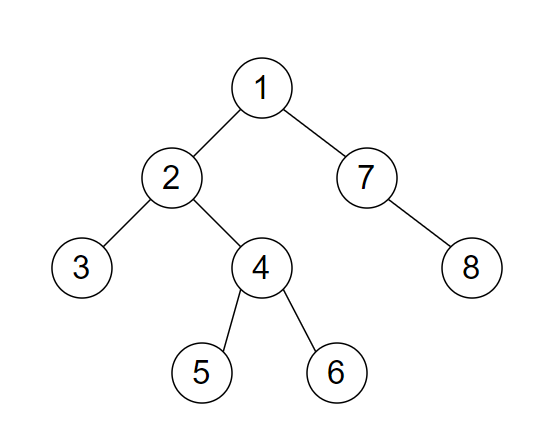
例えば下記のような木の場合に記録される配列は以下のようになる。
- 頂点に注目する場合は、探索した頂点を順番に配列に入れる。この時途中で経由する場合も配列に追加する。
- 辺に注目する場合は、探索した辺を探索した順番で配列に入れる。
- 上から下へ行く辺は +(下の頂点)
- 下から上へ行く辺は -(下の頂点)
- 根 (下図の 1) に向かう辺は存在しないが、あると仮定して記録を行う。
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 頂点 | 1 | 2 | 3 | 2 | 4 | 5 | 4 | 6 | 4 | 2 | 1 | 7 | 8 | 7 | 1 | - |
| 辺 | 1 | 2 | 3 | -3 | 4 | 5 | -5 | 6 | -6 | -4 | -2 | 7 | 8 | -8 | -7 | -1 |
具体例
頂点 \(i\) を根とする部分木に含まれる頂点
概要の木において頂点に注目してオイラーツアーを行い順番を記録する。この時各頂点 \(i\) について最初に通過した時刻と最後に通過した時刻 \(\textrm{in}[i], \textrm{out}[i]\) を同時に記録する。
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 頂点 | 1 | 2 | 3 | 2 | 4 | 5 | 4 | 6 | 4 | 2 | 1 | 7 | 8 | 7 | 1 |
| - | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| in | 0 | 1 | 2 | 4 | 5 | 7 | 11 | 12 |
| out | 14 | 9 | 2 | 8 | 5 | 7 | 13 | 12 |
このようにすると閉区間[\(\textrm{in}[i], \textrm{out}[i]\)] をみると頂点 \(i\) を根とする部分木の頂点を求めることができるようになる。
例えば頂点 2 の in, out は[1, 9] なので順番を記録した配列の index が[1,9] の範囲を見れば頂点 2 を根とする部分木の頂点を求めることができる。
LCA
オイラーツアーを利用して頂点の順番を記録するときにその頂点の深さも同時に記録をする。
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 頂点 | 1 | 2 | 3 | 2 | 4 | 5 | 4 | 6 | 4 | 2 | 1 | 7 | 8 | 7 | 1 |
| 深さ | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 2 | 1 | 0 | 1 | 2 | 1 | 0 |
| - | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| in | 0 | 1 | 2 | 4 | 5 | 7 | 11 | 12 |
| out | 14 | 9 | 2 | 8 | 5 | 7 | 13 | 12 |
ここでは頂点 3 と頂点 6 の LCA を求めることを考える。この時 LCA は「頂点 3 から頂点 6 に DFS 順に移動するときに通る最も根に近い頂点」であるため、頂点 3, 6 の in の値 2, 7 の範囲の内、最も深さが浅い頂点を求める 「区間最小値」を求める問題に帰着する。今回の場合は頂点 2(深さ 1) が最も根に近い頂点であるためであるため \(\textrm{LCA}(3, 6) = 2\) となる。
区間最小値を求めるにはセグメントツリー等を利用する。